DETERMINAMOS E INTERPRETAMOS DATOS DE LAS MEDIDAS DE TENDENCIA CENTRAL
Del 10 al 14 de Agosto
PARA DATOS NO AGRUPADOS
PARA DATOS AGRUPADOS
PREGUNTA RETADORA
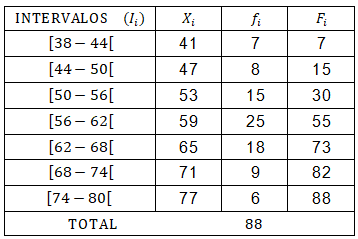
Se ha aplicado un
test de satisfacción en el trabajo a 88 empleados de una fábrica obteniéndose
la tabla de datos adjunta.
1) La media aritmética:
2) La mediana:
3) La moda


Buen día a todos; espero los desarrollos de la pregunta retadora
ResponderBorrarBuenas tardes profesor soy Milagros Oliver del 4to B, aquí está mi respuesta de la pregunta retadora.
ResponderBorrarA la tabla de frecuencia le he agregado una columna en la que he multiplicado la frecuencia absoluta por la marca de clase de cada intervalo y al final de la columna he sumado todos estos productos, este resultado me ha permitido hallar la media.
MEDIA:
Media = ∑(fi.Xi)/n
Media = 5204/88 = 59,14
MEDIANA:
Primero voy a identificar la clase media con n/2 = 88/2 = 44
Me= 56+44-30/25x6
Me= 56+0,56×6
Me= 56+3,36
Me= 59,36
MODA:
Δ₁ = fi-fi-₁
Δ₁ = 25-15
Δ₁ = 10
Δ₂ = fi-fi+₁
Δ₂ = 25-18
Δ₂ = 7
Mo= 56+10/17x6
Mo= 56+0.59x6
Mo= 56+3.54
Mo= 59,54
INTERPRETACIÓN:
- Media: El nivel de satisfacción del promedio de trabajadores es de 59,14
- Mediana: El 50% de trabajadores tiene un nivel de satisfacción por debajo del 59,36 y el otro 50% tiene un nivel de satisfacción por encima de 59,36
- Moda: El grupo más grande de trabajadores tiene un nivel de satisfacción de 59,54
Buen día Milagros; es correcto el planteamiento, desarrollo y tus resultados obtenidos, la interpretación en cada caso es el adecuado, felicito tu participación en esta oportunidad.
BorrarAsí como hay medidas de tendencia central, existen medidas de dispersión ¿Conoces algunas?
Buenas tardes profesor, si conozco algunas medidas de dispersión, estás son, rango (R), varianza (V), desviación estándar (S) y coeficiente de variación (CV).
BorrarBuen día Milagros; es correcto el planteamiento, desarrollo y tus resultados obtenidos, la interpretación en cada caso es el adecuado, felicito tu participación en esta oportunidad.
ResponderBorrarAsí como hay medidas de tendencia central, existen medidas de dispersión ¿Conoces algunas?
Buenas tardes profesor soy el alumno Jesús Terán del 4to "B"
ResponderBorrarMedia aritmética (Es el promedio de la situación):
∑(fi.Xi)/n
Me= 5204/88
Me= 59.136 = 59.14
Mediana (El valor central de la situación):
identifico la mediana = n/2=88/2=44
Me= 56+44-30/25x6
Me= 56+0.56×6
Me= 56+3.36
Me= 59.36
Moda (Es el dato con mayor frecuencia):
Mo= Li+(Δ1/Δ1+Δ2)*c
Δ1= fi-fi-1
Δ2= fi-fi-1
Δ1= 25-15
Δ1= 10
Δ2= 25-18
Δ2= 7
Mo= 56+10/17*6
Mo= 56+0.58*6
Mo= 56+3.48
Mo= 59.48
Buen día Jesùs; es correcto el planteamiento, desarrollo y tus resultados obtenidos, la interpretación en cada caso es el adecuado, felicito tu participación en esta oportunidad.
BorrarAsí como hay medidas de tendencia central, existen medidas de dispersión ¿Conoces algunas?
Buenas tardes profesor soy la alumna Lucia Isabel Quispe Minaya del 4B sec.
ResponderBorrarPREGUNTA RETADORA
Se ha aplicado un test de satisfacción en el trabajo a 88 empleados de una fábrica obteniéndose la tabla de datos adjunta.
HALLAR
1) La media aritmética
2) La mediana
3) La moda
DATOS
- En total son 88 empleados
-Tengo una tabla de frecuencias
OPERACION
*Media
x̄=(Σxi x fi)/N
Tengo que hallar la suma de los (xi)x(fi) = 5204
N(Σfi) = 88
Entonces ...
x̄=(5204)/88=59.14
________________________________
*Mediana
Me=Li+((N/2)-(fi-1)/fi)x ai
Me= 56+44-30/25x6
Me= 56+0,56×6
Me= 56+3,36
Me= 59,36
________________________________
*Moda
Mo=Li+(fi-fi-1/(fi-fi-1)+(fi-fi+1))x ai
Mo=6+(25-15)/(25-15)+(25-18))x6
Mo=59.54
RESPUESTA
-El promedio de satisfaccion de los trabajadores es:59.14
-La mediana del nivel de satisfaccion de los trabajadores es 59.36
-La mayoria de trabajadores tiene un nivel de satisfaccion de 59.54
Buen día Lucìa; es correcto el planteamiento, desarrollo y tus resultados obtenidos, la interpretación en cada caso es el adecuado, felicito tu participación en esta oportunidad.
BorrarAsí como hay medidas de tendencia central, existen medidas de dispersión ¿Conoces algunas?
Buenas tardes profesor SI
BorrarRANGO
El rango de un grupo de números es la diferencia entre el número mayor y el menor del grupo.
Varianza
VARIANZA
De una distribución de frecuencia la varianza puede ser obtenida de la fórmula.
DESVIACION ESTANDAR
La desviación estándar se define como: S√s²
COEFICIENTE DE VARIACION
La variación real o dispersión determinada a partir de la desviación estándar u otra medida de dispersión, es llamada la dispersión absoluta.
Si la dispersión absoluta es la desviación estándar S y el promedio, la dispersión relativa se llama coeficiente de variación o coeficiente de dispersión.
Buenos días profe, soy el alumno Zegarra del 4to "C"
ResponderBorrarPREGUNTA RETADORA
Se ha aplicado un test de satisfacción en el trabajo a 88 empleados de una fábrica obteniéndose la tabla de datos adjunta.
HALLAR
1) La media aritmética
2) La mediana
3) La moda
*Media
x̄=(Σxi x fi)/N
5204 (Σxi x fi)
88= N
Entonces ...
x̄=(5204)/88= 59.136
Al redondeo 59.14
x̄=59.14
*Mediana
Me=Li+((N/2)-(fi-1)/fi)x ai
Me= 56+44-30/25x6
Me= 56+0,56×6
Me= 56+3,36
Me= 59,36
*Moda
Mo=Li+(fi-fi-1/(fi-fi-1)+(fi-fi+1))x ai
Mo=6+(25-15)/(25-15)+(25-18))x6
Mo=59.54
RESPUESTA
-El promedio de satisfaccion de los trabajadores es:59.14
-La mediana del nivel de satisfaccion de los trabajadores es 59.36
-La mayoria de trabajadores tiene un nivel de satisfaccion de 59.54
Buen día Arturo; es correcto el planteamiento, desarrollo y tus resultados obtenidos, la interpretación en cada caso es el adecuado, felicito tu participación en esta oportunidad.
BorrarAsí como hay medidas de tendencia central, existen medidas de dispersión ¿Conoces algunas?
Buen día Arturo; es correcto el planteamiento, desarrollo y tus resultados obtenidos, la interpretación en cada caso es el adecuado, felicito tu participación en esta oportunidad.
ResponderBorrarAsí como hay medidas de tendencia central, existen medidas de dispersión ¿Conoces algunas?
Buenos noches profesor soy sebastian huamancaja del 4°C
ResponderBorrarRealizamos la distribución de frecuencias y el valor de la desviación estándar la obtenemos luego del calcular la media de la misma.
Media:
μ= Σxi*fi/n
μ = 5204/88
μ= 59,13
Desviación estándar:
σ= √∑(xi-μ)²/n
σ= √7845,44/88
σ= 9,44
hallamos la media, mediana y moda:
Moda
Mo=Li+(fi-fi-1/(fi-fi-1)+(fi-fi+1))x ai Mo=6+(25-15)/(25-15)+(25-18))x6 Mo=59.54
media
Me= 56+44-30/25x6 Me= 56+0,56×6 Me= 56+3,36 Me= 59,36-
meidana = n/2=88/2=44
Me= 56+44-30/25x6 Me= 56+0.56×6 Me= 56+3.36 Me= 59.36
Buenas noches profesor, soy el alumno Fernando Peña Jauregui de 4B
ResponderBorrarSe ha aplicado un test de satisfacción en el trabajo a 88 empleados de una fábrica obteniéndose la tabla de datos adjuntados.
El problema pide hallar la media, mediana y moda.
Media: x̄=(Σxi x fi)/N
Primero sumare todos los datos dentro de la columna (xi)x(fi) y eso da como resultado: 5204
N se sabe que es igual a la suma de todos los datos dentro de la columna fi: 88
Remplazamos datos:
x̄=(Σxi x fi)/N x̄=5204/88= 59.136 = 59.14
Mediana: Li+((N/2)-(fi-1)/fi)x ai
Resolvemos:
Mediana= 56 + 44 - 30/25 x 6
Mediana= 56 + 0,56 × 6
Mediana= 56 + 3,36
Mediana= 59,36
Moda: Li+(fi-fi-1/(fi-fi-1)+(fi-fi+1))x ai
Resolvemos:
Moda=6+ (25-15)/(25-15) + (25-18)) x6
Moda=59.54
Buenas noches profesor. Soy la alumna Daniela Pacheco de 4 "B"
ResponderBorrarSe ha aplicado un test de satisfacción en el trabajo a 88 empleados de una fábrica obteniéndose la tabla de datos adjunta.
1) La media aritmética:
Media = ∑(fi.Xi)/n
Media = 5204/88 = 59,14
2) La mediana:
n/2=88/2=44
Me= 56+44-30/25x6
Me= 56+0.56×6
Me= 56+3.36
Me= 59.36
3) La moda
Δ₁ = fi-fi-₁
Δ₁ = 25-15
Δ₁ = 10
Δ₂ = fi-fi+₁
Δ₂ = 25-18
Δ₂ = 7
Mo= 56+10/17x6
Mo= 56+0.59x6
Mo= 56+3.54
Mo= 59,54
Profesor buenas noches soy la alumna daphne de la cruz sava del 4B y aquí están mis respuesta de la pregunta retadora
ResponderBorrarMedia:
μ= Σxi*fi/n
μ = 5204/88
μ= 59,13
Desviación estándar:
σ= √∑(xi-μ)²/n
σ= √7845,44/88
σ= 9,44
El valor correspondiente a la desviación estándar es 9,44
Su esta mal me corrige por favor 😅
buenas tardes profesor soy karen alvaro del 4B
ResponderBorrarSe le aplicado el test de satisfacción para el trabajo a 88 empleados de la fábrica obteniendo la tabla de datos
1) La media aritmética:
Media = ∑(fi.Xi)/n
Media = 5204/88 = 59,14
2) La mediana:
n/2=88/2=44
Me= 56+44-30/25x6
Me= 56+0.56×6
Me= 56+3.36
Me= 59.36
3) La moda
Δ₁ = fi-fi-₁
Δ₁ = 25-15
Δ₁ = 10
Δ₂ = fi-fi+₁
Δ₂ = 25-18
Δ₂ = 7
Mo= 56+10/17x6
Mo= 56+0.59x6
Mo= 56+3.54
Mo= 59,5
Buenos días profesor, soy el alumno Rodrigo Kento Cabrera Cajacuri del 4to C. Lamento la tardanza en la entrega de la tarea.
ResponderBorrar1. Media aritmética.
Me= ∑(fi.Xi)/n
Me = [(41*7) + (47*8) + (53*15) + (59*25) + (65*18) + (71*9) + (77*6)]/88
Me= 5204/88
Me= 59,14
2. Mediana.
Mediana: Li+((N/2)-(fi-1)/fi)x ai
Mediana= 56 + 44 - 30/25 x 6
Mediana= 56 + 0,56 × 6
Mediana= 56 + 3,36
Mediana= 59,36
3. Moda.
Mo= Li+(fi-fi-1/(fi-fi-1)+(fi-fi+1))x ai
Mo=6+ (25-15)/(25-15) + (25-18)) x6
Mo=59.54
Buenos noches profesor soy la alumna Fuentes del 4"C" y esta es mi respuesta:
ResponderBorrar*Media
x̄=(Σxi x fi)/N
5204 (Σxi x fi)
88= N
Entonces ...
x̄=(5204)/88= 59.136
Al redondeo 59.14
x̄=59.14
*Mediana
Me=Li+((N/2)-(fi-1)/fi)x ai
Me= 56+44-30/25x6
Me= 56+0,56×6
Me= 56+3,36
Me= 59,36
*Moda
Mo=Li+(fi-fi-1/(fi-fi-1)+(fi-fi+1))x ai
Mo=6+(25-15)/(25-15)+(25-18))x6
Mo=59.54
Rpta:-El promedio de satisfacción de los trabajadores es:59.14
-La mediana del nivel de satisfacción de los trabajadores es 59.36
-La mayoría de trabajadores tiene un nivel de satisfacción de 59.54