SÓLIDOS GEOMÉTRICOS(Continuación)
SEMANA 36: Del 07 al 11 de diciembre
Normas de convivencia:
-Ingresamos a la reunión saludando
-Respetamos a todos y somos empáticos
-Pedimos la palabra para poder intervenir en la reunión
-Colocamos nuestra asistencia en el formulario.
PROPÓSITO. Expresarás con lenguaje geométrico la comprensión sobre las propiedades de las formas tridimensionales. Además, combinarás estrategias para calcular el área y volumen de formas tridimensionales como el prisma y paralelepípedo, y plantearás afirmaciones sobre estos.
ÁREA Y VOLUMEN DE UN PRISMA
CUERPOS DE REVOLUCIÓN
PREGUNTA RETADORA
Halle el área y volumen de la siguiente figura compuesta:
DIRECCIÓN DE TAREAS DE LA SEMANA 36:
4° B:
LA DIRECCIÓN DE TAREAS ESTÁ EN LOS COMENTARIOS
4° C:
LA DIRECCIÓN DE TAREAS ESTÁ EN LOS COMENTARIOS
Buenos días a todos; espero sus participaciones en esta última semana 36, a través de la pregunta retadora.
ResponderBorrarDIRECCIÓN DE TAREAS DE LA SEMANA 36:
ResponderBorrar4° B:
https://docs.google.com/forms/d/1S2kqurGM-6dK3Gu9jw0vy0tAYokqy7JlcUozZvYh0Ig/edit
4° C:
https://docs.google.com/forms/d/1TunTbY_L0vEWapLzJR_8SOHKyRL02ED6L9aAqRVwit8/edit
Buenas tardes profesor, soy Jeyson Yohan Mitma Rosado del 4 B
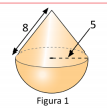
ResponderBorrarHalle el área y volumen de la siguiente figura compuesta:
AREAS:
-Cono: 8^2= c^2 + 5^2
64= c^2+25
-25+64= c^2
raíz de 39=c ...... =6.244=6.2
A= 3.14x5x6.2=97.34 cm2
-Semi esfera: 1/2x4(3.14)x5 = 31.4 cm2
AREA TOTAL= 31.4 + 97.34= 128.74 cm2
VOLUMEN:
-CONO: 1/3 X 5^2(3.14) X 6.2= 162.23 cm3 PERIÓDICO PURO
-SEMIESFERA: 1/2 X 4/3 X 3.14 X 125= 261.66 cm3
VOLUMEN TOTAL= 261.66+162.23= 423.89 cm3
eso es todo profesor, gracias.
Buenas tardes profesor soy Lucia Quispe Minaya del 4to "B" sec.
ResponderBorrarPREGUNTA RETADORA
Halle el área y volumen de la siguiente figura compuesta:
1.- Primero debemos hallar la altura de la figura
h^2 = 8^2 - 5^2 = 39
h = raiz cuadrada de 39 = 6,2
2.- Luego hallamos el volumen del cono que esta encima
Vc = (Area de la base x H) / 3
Vc = (3.14 x 5^2 x 6,2) / 3
Vc = 162.3 cm^3
3.- Luego hallamos el voulmen de la semi esfera
Vs.e = (4 x 3.14 x 5^3) / 3
Vs.e = 523.3
Vs.e = 523.3 / 2
Vs.e = 261.7
4.- Sumamos ambos volumenes para hallar el total
Vt = 162.3 + 261.7 = 424 cm^3